Xiangyu Hu

Puzzle on the origin of numerical instability

This blog is based on parts from the Journal of Computational Physics paper, “Essentially non-hourglass SPH elastic dynamics”, Volume 510, 1 August 2024, 113072.

More than two decades ago, it was found that the numerical simulations of typical elastic dynamics problems using updated Lagrangian smoothed particle hydrodynamics (ULSPH) may lead to numerical instability.

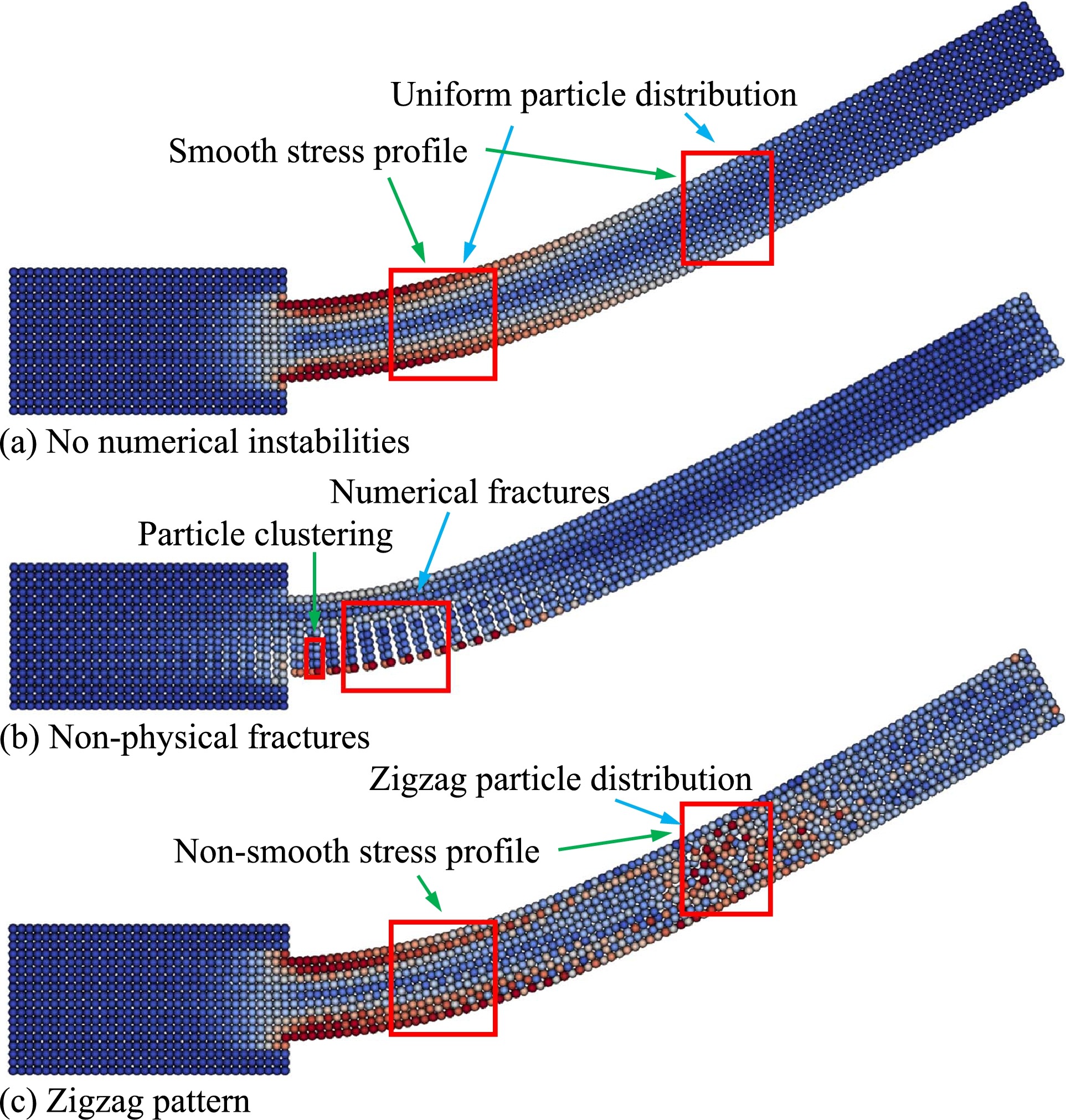
Tensor-instability

Fig. 1. Illustration for (a) no numerical instabilities, (b) non-physical fractures and (c) zigzag pattern in ULSPH simulations of 2D oscillating plates. The particles are colored with von Mises stress.

Tensile instability

As shown in Fig. 1b for a typical example, the numerical instability involving particle clustering and non-physical fractures presented in these simulations is often identified as tensile instability, a fundamental numerical issue caused by the tensile stress. Such instability often exhibit also in fluid simulations when negative pressure exists. Since such numerical instability is identified, different approaches have been proposed to eliminate or suppress it. One popular method is the artificial stress method, based on the concept of counteracting the tension with compressive stress an hence preventing the instability.

Hourglass modes

An interest phenomenon one can observe is that, as shown in Fig. 1c, although the artificial stress can eliminate non-physical fractures in some cases, the artifacts with zigzag patterns appear in the stress profile. This issue is not unique for the specific cases, and can be found in other ULSPH methods aimed at mitigating tensile instability. The zigzag pattern is a typical numerical instability phenomenon well known as hourglass modes, another fundamental numerical issue related to collocation methods. Hourglass modes were also found in total Lagrangian SPH (TLSPH) elastic dynamics, when the deformation is very large, even though TLSPH does not suffer from the tensile instability, i.e. without particle clustering and non-physical fractures.

Origin of the numerical instability

The above observations lead to people puzzling which is the original mechanism of the instability shown in SPH solid dynamics simulations. Is the tensile instability or actually the hourglass modes?. In the next part, I will introduce the approach developed in the above journal paper which is able to resolve this puzzle.