Xiangyu Hu

Remedy for hourglass modes

Since the method for preventing tensile instability is still not able to eliminate the zigzag artifact (characteristic for hourglass modes), it is quite rational to propose that both instabilities have contributions rather than that of tensile instability only. Furthermore, this does not exclude the possibility that only hourglass modes contribute the instability observed in these numerical simulations.

If only the hourglass modes have contribution, one may require that all the numerical simulations which are identified as tensile instability become numerically stable if only the method preventing hourglass is applied.

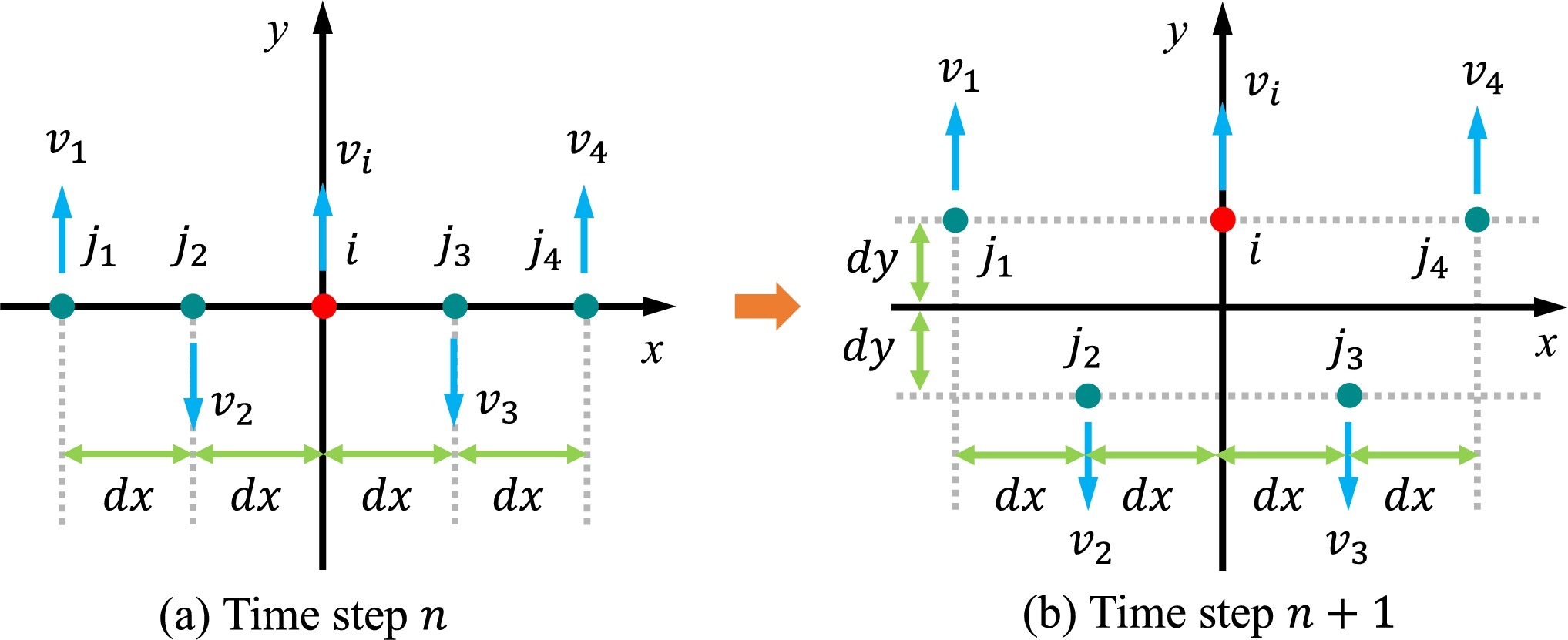
Zigzag

Fig. 2. Illustration of zero energy modes by considering a simple case. The particles are uniformly distributed along the x-axis, and change from time step n to time step n + 1 with the velocity perpendicular to the x-axis.

Origin of hourglass modes

In standard SPH method, the strain of a particle $i$ is integrated from the velocity gradient approximated as \({\nabla_i \mathbf v}=\sum_{j} \mathbf v_{ij} \otimes {\nabla_i W_{ij}} V_j.\) This approximation generally works well but may fail in some specific velocity field, and leads to the hourglass (or zero energy) modes. As shown in Fig. 2, we use a simple case to demonstrate this issue. The particles are uniformly distributed along the $x$-axis, and the particles change from time step $n$ to time step with the velocity profile characterized with a zigzag pattern. Under such circumstance, the above original SPH formulation yields a artificial zero velocity gradient, or zero elastic-energy for particle $i$, consequently leading to a negligible stress increment. In other words, this deformation mode is not resisted with elastic force and, naturally, cannot recover even under large deformation conditions, which leads to an inaccurate estimation of the shear stress and shear acceleration.

Non-nested formulation of shear force

In a recent effective remedy for hourglass modes in our previous journal paper on total Lagrangian SPH (TLSPH) method, the particle acceleration due to the shear stress is directly obtained from a one-step Laplacian formulation of the particle displacement other than the nested implementation of the 2nd-order derivatives used in the previous TLSPH formulations. Actually, such non-nested SPH formulation of Laplacian is widely used in SPH fluid dynamics for computing the viscous-force term in the Navier-Stokes equations, and is found much stabler than the nested counterpart.

In the journal paper, with very similar idea, we present an essentially non-hourglass formulation by utilizing the Laplacian operator which is widely used in fluid simulations. The final non-nested formulation of shear acceleration can be written as

\({\dot{\mathbf v}^s} = 2 \zeta {\frac{G}{\mathbf \rho} {\int_{0}^{t} {\left(\sum_{j} \frac{\mathbf e_{ij} \cdot \mathbf v_{ij}}{r_{ij}} {\nabla_i W_{ij}} V_j \right)} \text{d}t}}\) Compared to the original SPH methods, this formula is capable of eliminating zero energy modes, i.e., it can account for the variations in shear acceleration caused by the deformation illustrated in Fig. 2 since every particle pair has contribution to shear force induced acceleration.

For the detailed derivation, one can refer to the journal paper.

Is the remedy able to eliminate tensile instability?

From the above formulation, we see that the shear deformation in zigzag particle distribution generates sufficient shear force to avoid the zero energy modes. In the next part, I will demonstrate that it is not only able to eliminate the hourglass modes, but also the instability previous considered as tensile instability.